Lab 06

In this lab session you will be practicing the basic JUnit syntax, allowing you to write simple unit tests, including special conditions like timeouts and exceptions. For this exercise you'll be working with several prepared codebases. The git clone instructions for the code needed are included throughout the remainder of this guide.

Perfect numbers

Perfect numbers are positives for which the sum of all divisors (including 1) adds up to the number itself.
Perfect numbers are rare, they are a lot harder to find than primes.
The first four perfect numbers are: 6, 28, 496, 8128.
Here is a link to primitive perfect number checker. It will be your task to implement some basic tests.

Info

It is not known whether there are any odd perfect numbers, nor whether infinitely many perfect numbers exist. If you found a proof for either, let me know and I'll ensure you get an amazing scholarship.

Basic unit tests

Unit tests are methods, fulfilling the following conditions:

Method signature starts with public void.
Method is decorated with @Test annotation.
Method is placed in a class of the src/test/java subfolder (for maven projects).

For the first exercise you'll have to write unit tests for a provided implementation. To prepare the task, setup the provided Perfect number analyzer:

Clone the project: git clone https://gitlab.info.uqam.ca/inf2050/perfectnumbers.git
Open the project in IntelliJ
Launch it with: mvn clean compile exec:java
The project will compute the first 4 perfect numbers, then stop.

Your turn

Time to write some basic unit tests.

Open the prepared class, and locate the existing unit test:

 @Test
 public void findFirstFourPerfectNumbers() throws PerfectNumberLimitException {
   PerfectNumberAnalyzer analyzer = new PerfectNumberAnalyzer();
   int[] firstFour = analyzer.findPerfectNumbers(4);
   int[] expectedResult = new int[] {6, 28, 496, 8128};
   Assert.assertArrayEquals("Numbers computed by analyzer are incorrect!", expectedResult, firstFour);
 }

In IntelliJ: Navigate to the file-system representation on the left. Right-click on the test package (ca.uqam.info), and select Run Tests in info.
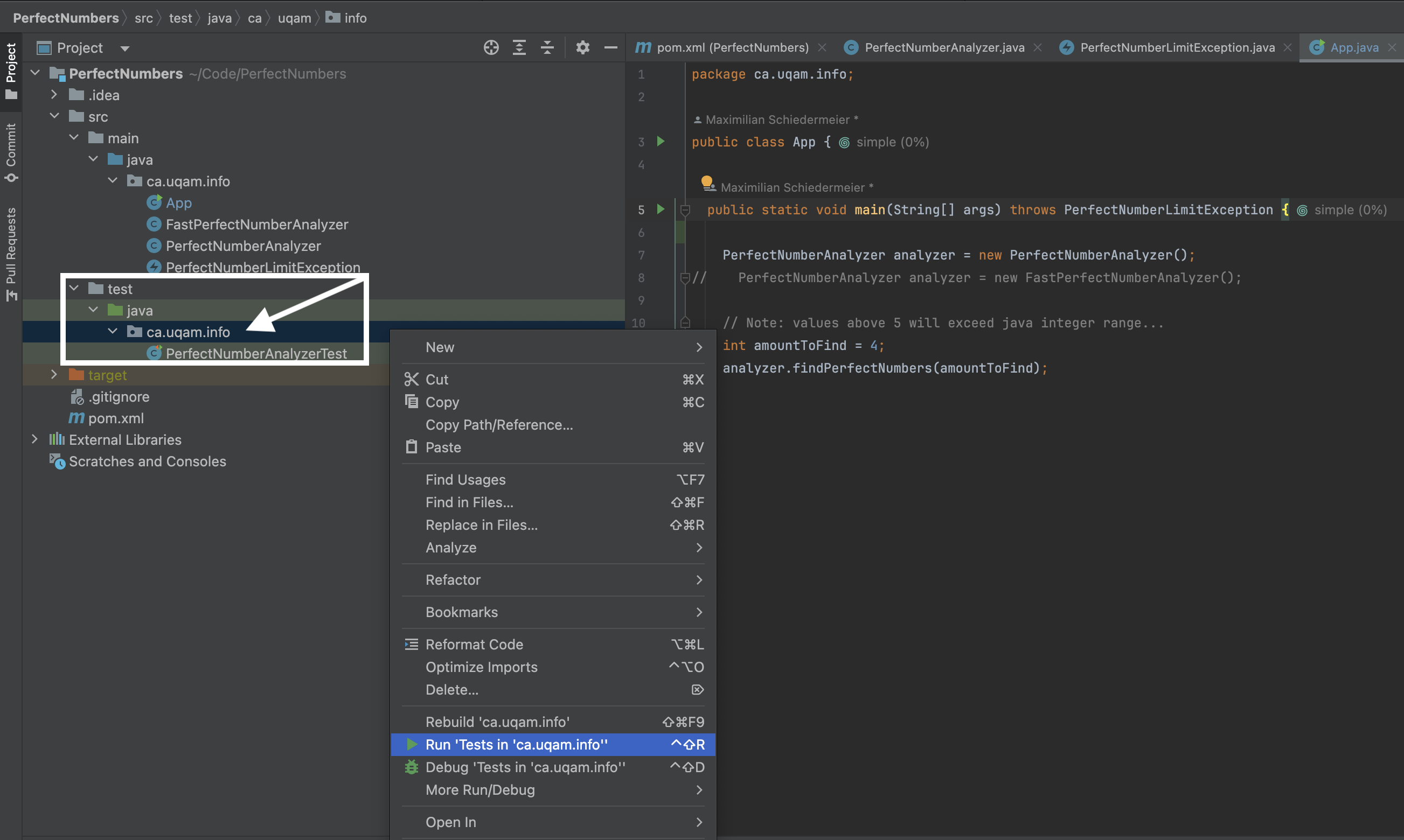
Verify that your first test passes.

Next we want to add a time constraint:

Add a copy of the test, that verifies for the first 5 perfect numbers !
- The 5th perfect number is: 33550336
The test will take very long to succeed (about 15 minutes). That's because the 5th perfect number is a lot larger. Checking 33 million numbers takes a while.
Clearly we do not have that much patience, so we want the test to fail if the 5th number has not been found within a second.
- Modify the @Test annotation to set an upper threshold of 1000 milliseconds
- Run the tests again, and make sure the test result appear within a second.
- The second test should now fail.

Regression tests

Regression testing is about ensuring that additional functionality does not break anything that previously already has been working.
- Now we want to improve, the existing search for perfect numbers
- But we also want to make sure we do not regress!

Your turn

Here's a class that searches for perfect numbers a lot faster.

package ca.uqam.info;

/**
 * Faster extension for perfect number analyzer. Searches only numbers by constructing candidates
 * in binary representation.
 *
 * @author Maximilian Schiedermeier
 */
public class FastPerfectNumberAnalyzer extends PerfectNumberAnalyzer {

  /**
   * Provides the next number to test. Default implementation tests all numbers, i.e. each iteration
   * is just the number itself. Uses binary formula to find perfect number candidates. All perfect
   * numbers are of form 1....10.....0, which one more "1"s than "0"s.
   * Examples: 110, 11100, 1111000, ...
   *
   * @param iteration as the amount of 0s to contain
   * @return decimal equivalent of the binary constructed candidate.
   */
  protected int getNextNumberToTest(int iteration) {

    String binaryNumber = "1";
    for (int j = 0; j < iteration; j++) {
      binaryNumber = "1" + binaryNumber;
      binaryNumber = binaryNumber + "0";
    }
    return Integer.parseInt(binaryNumber, 2);
  }
}

Why would that be a valid approach?

The first four perfect numbers in binary are: 110, 11100, 11111000000, 1111111000000 ... do you see a pattern ? The improved algorithm constructs candidates in binary and only checks those candidates. That's a lot faster than checking all numbers!

Add the above class to your project.
Modify App.java to use FastPerfectNumberAnalyzer instead of `PerfectNumberAnalyser, and search for the first 5 instead of the first 4 perfect numbers.
Add a new unit tests findFirstFivePerfectNumbersFast to PerfectNumberAnalyzerTest that checks for the first 5 perfect numbers, using the Fast implementation.

Test timeout

In class, you've seen how to "decorate" @Test annotations, to consider additional constraints.
Find the syntax to set an upper time limit for execution of a test.

Your turn

Modify the previously implemented findFirstFivePerfectNumbersFast test, and add a time constraint.
- It must fail if it takes longer than 0.1 seconds.
Launch your tests, and verify that it passes, using the fast search implementation.
Modify your test to use the slow search implementation, and verify it will fail. Then switch back to the fast implementation.

Expecting exception

Perfect numbers are pretty "rare".
- The sixth number is already, 8.589.869.056, which is greater than the maximum java integer value (2.147.483.647).
Both implementations, have a safety check that refuses execution when more than 5 numbers are requested.
- It would be best to also test if the safety check is correctly implemented.
- Correctly implemented means: the program will throw an PerfectNumberLimitException, when requested to search for more than 5 perfect numbers.
Find the syntax to check for a thrown exception during execution of a test.

Your turn

Add a test findFirstFivePerfectNumbersFast, that attempts to search for the first 6 perfect numbers.
If executed the test will fail with an exception.
Modify the test to only pass if a PerfectNumberLimitException is thrown.

Stateful tests

Test must work in any order.

That is not a big deal when working with mathematical functions (e.g. checking for perfect numbers).
Every test creates a new object instance, therefore working with stateful objects is not an issue either. Every tests lives in its own object sandbox.
But sometimes you are working with objects that persist state externally, i.e. databases.

For the following tasks you will be working with the StudentDatabase sample project, available on GitLab.

Create a "DataBase" on your Desktop:
- Filename: studentdb.txt
- Content: "Max Ryan Quentin Romain"
Clone the StudentDatabase sample project code, and open it in IntelliJ
- git clone https://gitlab.info.uqam.ca/inf2050/DataBaseTesting.git

After

Another issue with databases, is that tests are no longer independent.
Even though JUnit creates a new test class instance for every method annotated with @Test, the data is persisted outside the class. Therefore tests altering state easily conflict with one another.

Your turn

Add two additional individual tests:
- testAddStudent(), which calls TextDatabase.addStudent("Hafedh"). Followed by a database read and verification that Hafedh has been added and the list now contains 5 students.
- testRemoveStudent(), which calls TextDatabase.removeStudent("Max"). Followed by a database read and verification that Max has been removed and the list now contains 3 students.
When you run all tests, some will fail, because the tests are no longer independent.
Revisit the course content and find an extra annotation to declare a method to be executed after each test.
- Write a helper method that cleans up the database after every test, so there are no more dependencies.

Before

Before you can test CRUD (Create Read Update Delete) operations, you need a database connection.
If you inspect your code, every of your tests has begun with the same line, establishing a connection, followed by the actual test.
But that is pure boilerplate code and duplicated across all tests !
Much better is to automatically ensure the DB connection is established before every individual test.

Your turn

Open the DataBaseTesting class, and ensure you can run the provided testDatabaseRead test.
Refactor the code:
- Add a new private field to the class: private TestDatabase studentDatabase;
- Refactor the test's first line to an extra method, e.g. named connectToDatabase().
- Revisit the last lecture's content and find which annotation to add to the newly created method, to ensure it is invoked before every test.
Ensure you can still run the test.

Coverage

Tests are a great way to identify bugs, but unfortunately they tell you little about the absence of bugs.
While it is not trivial to get certainty on the quality of tests, there are some ways to check of tests are at least somewhat wholesome, regarding the codebase
The standard metric is coverage.
In IntelliJ you can create a coverage report, by right-clicking on the test package, followed by More Run/Debug -> Run tests with coverage...

Database coverage

In this exercise you'll be measuring the test coverage of your existing student database project.

Your turn

Create a coverage report for your database production code.
It will output a line coverage of 95%.
Find the line(s) that were not covered

Inspect the line markers

Once a coverage report has been generated, every executable line has a coloured marker. Search for lines with a red marker.

Monkey tests

Monkey tests are useful to scale up testing with random inputs. However, asserting for random numbers can be a bit tricky. In this last exercise you'll practice implementing monkey tests on the example of a simple prime number checker.

Checking prime numbers

Assume there's a need for a class PrimeChecker, with a single method public boolean isPrime(int numberToTest).
- The method is supposed to return true for prime numbers and false for non-prime numbers.

You followed a Test-Driven-Development approach and first implemented the corresponding unit test:

package ca.uqam.info;

import org.junit.Assert;
import org.junit.Test;

public class PrimeCheckerTest {

  @Test
  public void verifySomeKnownResults() {
    Assert.assertFalse("4 is not a prime, but checker said it were.", PrimeChecker.isPrime(4));
    Assert.assertTrue("5 is a prime, but checker said it were not.", PrimeChecker.isPrime(5));
    Assert.assertFalse("10 is not a prime, but checker said it were.", PrimeChecker.isPrime(10));
    Assert.assertTrue("13 is a prime, but checker said it were not.", PrimeChecker.isPrime(13));
  }
}

However, the test can be easily outsmarted. E.g. the below fake program can be used to pretend the task were solved:

  public static boolean isPrime(int numberToTest) {

  if (numberToTest == 4) {
    return false;
  }
  if (numberToTest == 5) {
    return true;
  }
  if (numberToTest == 10) {
    return false;
  }
  return true;
}

Your turn

Implement a monkey test, that generates 1000 pseudo random numbers and tests the implementation.
Since you do not want to reimplement the primechecker in your test, make conditional assertments:
- If the number is even, or divisible by 3, expect false.
- Otherwise, make no assertions.

To get started, here is a code snipped to generate random positive numbers

Random randomNumberGenerator = new Random(42);
int randomNumber1 = Math.abs(randomNumberGenerator.nextInt());
int randomNumber2 = Math.abs(randomNumberGenerator.nextInt());
int randomNumber3 = Math.abs(randomNumberGenerator.nextInt());
...

Make sure that:

Your monkey test fails the above fake isPrime implementation.
Your monkey test does not fail an earnest isPrime implementation, e.g. the one below:

  public static boolean isPrime(int numberToTest) {
  if (numberToTest < 2) {
    throw new RuntimeException("Cowardly refusing to check number below 2.");
  }

  for (int i = 2; i * i <= numberToTest; i++) {
    if (numberToTest % i == 0) {
      return false;
    }
  }
  return true;
}